Recta numérica
La recta numérica, inventada por John Wallis, es un dibujo unidimensional de una línea en la que los números enteros son mostrados como puntos especialmente marcados espaciados uniformemente. Aunque la imagen de abajo muestra solamente los números enteros a entre -9 y 9, la recta incluye todos los números reales, continuando "ilimitadamente" en cada dirección. Frecuente es usada como ayuda para enseñar la adición y la sustracción simples, implicando especialmente números negativos.
Está dividida en dos mitades simétricas por el origen, es decir el número cero. En la recta numérica mostrada arriba, los números negativos se representan en rojo y los positivos en azul.
Ejemplo
Represente en la recta numérica los siguientes números racionales:
| |
Solución:
![]()
Ejercicio
1. Represente en un recta numérica los siguientes números racionales:
| |
2. Represente en una recta numérica los siguientes números racionales.
racionales y represéntelos en una recta numérica.
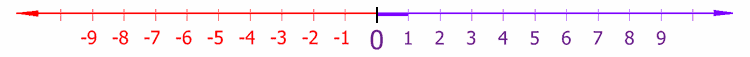

No hay comentarios:
Publicar un comentario